Boolean Propositional Logic for software installations.

Have you ever worked on a software development project, whether it was a small personal project to learn new skills or a large application running in production? If yes, then you have most likely used a package manager to install libraries or dependencies.

In this blog post, we explore how Boolean Propositional Logic can be used for package management within software development. To make things more interactive, we have also included a small game where you can act as a package manager yourself.

What is a Boolean Propositional Formula?

A Boolean Propositional formula consists of variables \(x_1, \dots , x_n\) and can be one of the following:

1. True
2. False
3. \(x_i\) for some \(i\)
4. \(\neg x_i\) for some \(i\); if \(x_i = True\) for some \(i\), then \(\neg x_i = False\)
5. \(F \lor G\) where F and G are formulas. This is referred to as OR or disjunction
6. \(F \land G\) where F and G are formulas. This is referred to as AND or conjunction
7. \(F \implies G\) where F and G are formulas. This is referred to as implication, which is equivalent to \(\neg F \lor G\)

What is a package manager?

A package manager is like an app store for developers, but instead of downloading games or social media apps, it helps them download pieces of code (called packages) that someone else has already written to solve common problems. They can now use this downloaded code to build new stuff upon it.

Imagine you're cooking a complex meal. You need salt, pepper, pasta, sauce, etc. Instead of growing tomatoes or grinding flour yourself, you just go to the store and buy what you need.

A package manager is that store for developers. It helps them:

• Find the ingredients (code libraries) they need.
• Download and install them quickly.
• Keep them up to date.
• Make sure all ingredients work well together (handle compatibility).

Here, we proceed with an example of a conda package manager. However, the same concepts apply to many other package managers as well. Say, we want to install a package named numpy via the conda package manager. We do this via conda install numpy :

The above video shows what happens after we enter the command conda install numpy in a terminal. But, where is the boolean logic involved here? Do you observe the list of other packages populated by conda that it wants to install? These are the packages that are kind of prerequisites for the numpy package to work properly and are called dependencies. A Boolean formula is used to determine this list of packages. Let us explore how the Boolean formula is leveraged here and if the task is as easy as it looks in the animation above.

Scenario

Say, we want to install a package named Alpha with version 2.0 (together, we refer to it as Alpha-2.0). The developers of Alpha-2.0 specify that their package uses functionalities from the following other packages:

1. Beta; either of Beta-1.3 or Beta-1.4 works.
2. Gamma; either of Gamma-0.6 or Gamma-0.7 works.

Based on the above specification, we say that Alpha-2.0 depends on Beta with version 1.3 or 1.4 and on Gamma with version 0.6 or 0.7.

However, the developers of Beta specify that their package is also dependent on the functionalities of Gamma in the following manner:

1. Beta-1.3 is dependent on Gamma-0.5.
2. Beta-1.4 is dependent on Gamma-0.6.

Info

When we say that alpha-2.0 depends on either Beta-1.3 or Beta-1.4, it could be that alpha-2.0 uses the functionalities common to both Beta-1.3 and Beta-1.4 and not the ones that are new in Beta-1.4. So, we can either install Beta-1.3 or Beta-1.4, but not both at the same time.

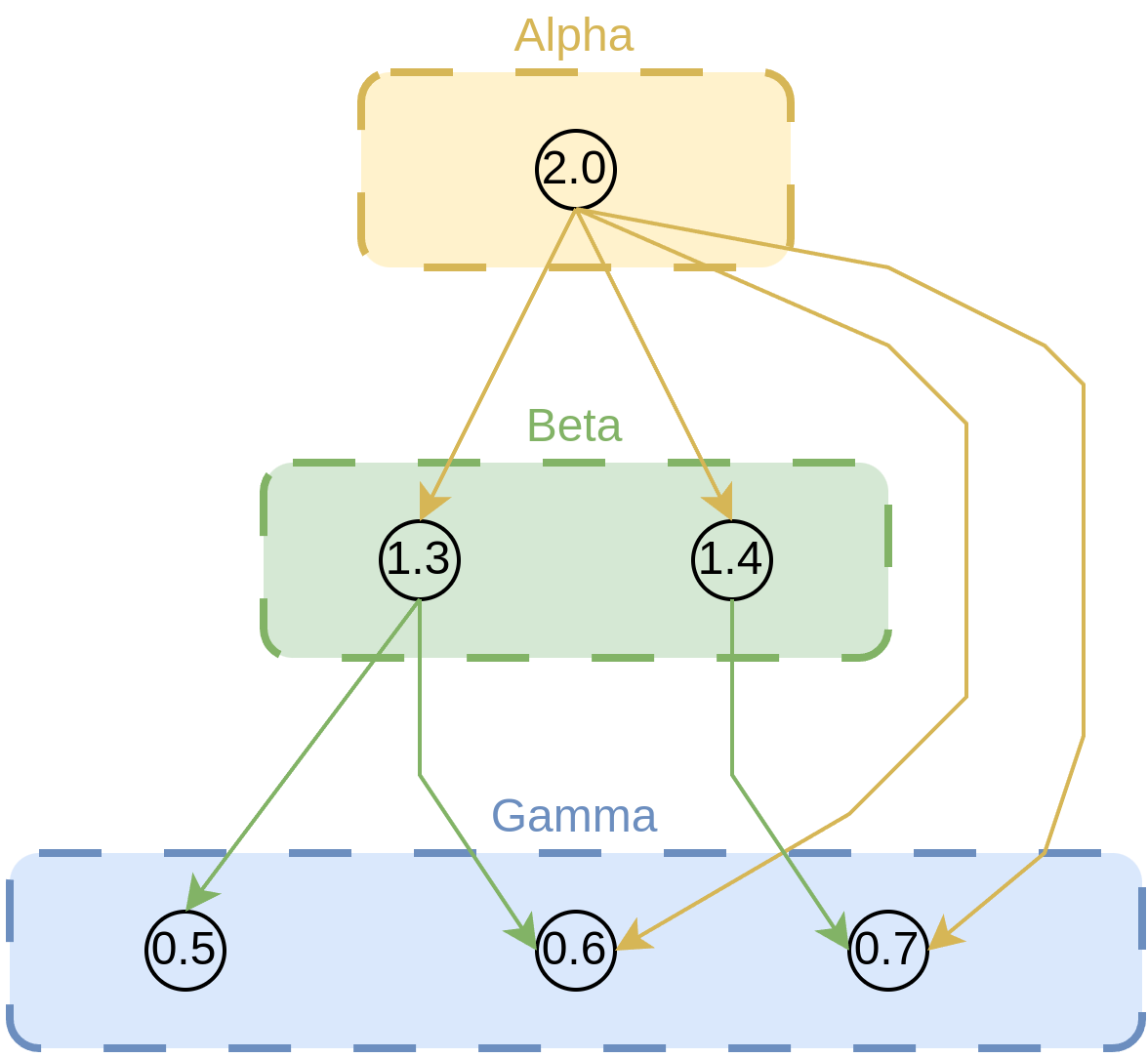
The above dependencies can be depicted via the diagram shown in Figure 1. To create the graph, we assume each version-specific package is a separate package (for example, we consider Beta-1.3 and Beta-1.4 as different packages) and represent them as vertices. And we create a directed edge from the package to another version-specific package on which the former depends.

Figure 1. Dependency graph: A graph depicting the dependencies of the packages. Each box represents a package and each circle inside the box represents a version. We can consider each package and version combination as a different package altogether. Hence, we consider a version-specific package (e.g. Beta-1.4) as a vertex and create a directed edge from the package to another version-specific package on which the former depends on.

Now, our objective is to pick the packages and versions to be installed in a way such that:

1. For each package, only one version is installed to ensure consistency.
2. All dependencies are satisfied.

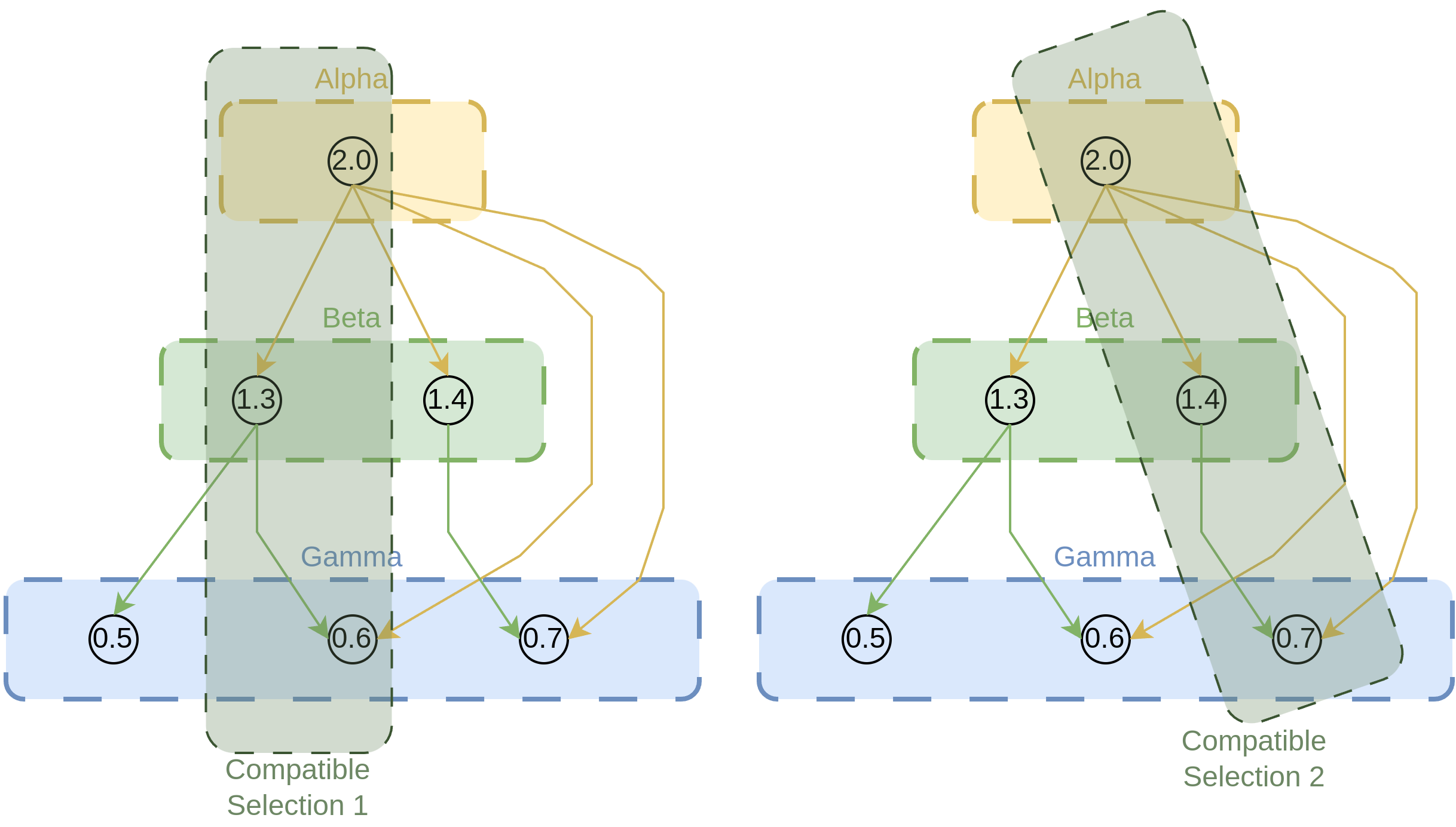
Given the above conditions, we can observe in Figure 2 that there are two compatible selections of packages:

1. Alpha-2.0, Beta-1.3 and Gamma-0.6
2. Alpha-2.0, Beta-1.4, and Gamma-0.7

Figure 2. Based on our conditions and dependencies, we can have two compatible selections: (i) Alpha-2.0, Beta-1.3 and Gamma-0.6, and (ii) Alpha-2.0, Beta-1.4, Gamma-0.7

Given the simplicity of the problem in terms of the number of packages and dependencies, we were able to find the selection easily and visually. But how to formally find the selection for a large number of packages and dependencies? And, how does a package manager do it? The answer is Boolean logic. So, let us now find how to transform the problem into a Boolean formula.

Transforming dependency requirements to logical formula

Step 1: We represent each version-specific package as a boolean variable, which can be either True or False. When the variable for the package is True, then the package is picked for installation, and if False, then it is not picked. For our example, we have 6 different variables as follows: Alpha1.0, Beta1.3, Beta1.4, Gamma0.5, Gamma0.6, and Gamma0.7.

Step 2: Each dependency can be represented using implications. For example, if \(A\) depends on \(B\) then we say, \(A \implies B\) which means that if \(A\) is installed then \(B\) must be installed and if \(A\) need not be installed then it doesn’t matter if \(B\) is installed or not. The dependencies in our example can be represented as follows:

1. \(Alpha2.0 \implies (Beta1.3 \lor Beta1.4)\)
2. \(Alpha2.0 \implies (Gamma0.6 \lor Gamma0.7)\)
3. \(Beta1.3 \implies (Gamma0.5 \lor Gamma0.6)\)
4. \(Beta1.4 \implies Gamma0.7\)

Step 3: To ensure that we have exactly one version of each package, we negate conjunctions of each unordered pair of versions of the same package. Say we have a package A with versions 1 and 2. The boolean formula to ensure a single version would be \(\neg (A1 \land A2)\), This ensures that \(A1\) and \(A2\) cannot be simultaneously True. For our example, we have the following conjunctions:

1. \(\neg (Beta1.3 \land Beta1.4)\)
2. \(\neg (Gamma0.5 \land Gamma0.6)\)
3. \(\neg (Gamma0.6 \land Gamma0.7)\)
4. \(\neg (Gamma0.5 \land Gamma0.7)\)

Now, if we create a conjunction of all four formulas above, we ensure that no two versions of the package become True or get installed at the same time. The conjunction of the above four terms would look like:

\[ \neg (Beta1.3 \land Beta1.4) \land \neg (Gamma0.5 \land Gamma0.6) \land \neg (Gamma0.6 \land Gamma0.7) \land \neg (Gamma0.5 \land Gamma0.7) \]

Step 4: Now we create a conjunction of all the terms in Step 1, Step 2, and Step 3, which will result in the following formula:

\[ [Alpha2.0 \implies (Beta1.3 \lor Beta1.4)] \land \\ [Alpha2.0 \implies (Gamma0.6 \lor Gamma0.7)] \land \\ [Beta1.3 \implies (Gamma0.5 \lor Gamma0.6)] \land \\ (Beta1.4 \implies Gamma0.7) \land \\ \neg (Beta1.3 \land Beta1.4) \land \neg (Gamma0.5 \land Gamma0.6) \land \\ \neg (Gamma0.6 \land Gamma0.7) \land \neg (Gamma0.5 \land Gamma0.7) \]

Step 5: The most important point is that Alpha-2.0 must be installed. Hence, the variable corresponding to it must always be assigned True i.e \(Alpha2.0 = True\). So, we create a conjunction of \(Alpha2.0\) with the formula in step 4:

\[ Alpha2.0 \land [Alpha2.0 \implies (Beta1.3 \lor Beta1.4)] \land \\ [Alpha2.0 \implies (Gamma0.6 \lor Gamma0.7)] \land \\ [Beta1.3 \implies (Gamma0.5 \lor Gamma0.6)] \land \\ (Beta1.4 \implies Gamma0.7) \land \\ \neg (Beta1.3 \land Beta1.4) \land \neg (Gamma0.5 \land Gamma0.6) \land \\ \neg (Gamma0.6 \land Gamma0.7) \land \neg (Gamma0.5 \land Gamma0.7) \]

Now, we just want an assignment of boolean values to each of the variables such that the formula evaluates to True. Packages corresponding to variables with True values will be selected for installation. This problem of finding a possible assignment of values to the Boolean variables such that the formula evaluates to True is called the Functional Boolean Satisfiability (FSAT) Problem. A simple extension/simplification of the problem is to decide if a Boolean formula is satisfiable or not, which is known as the Boolean Satisfiability (SAT) Problem. If we can find a solution for an instance of the FSAT problem, then we can say that the boolean formula is satisfiable, and if we can’t, we say the formula is unsatisfiable.

Before thinking about how to solve the problem, let us first verify if a solution (compatible selection of packages) we found in Figure 2 evaluates to True. Since the formula is quite long, we will evaluate each term of the conjunction separately and then evaluate the final result. For the conjunction to be True, all the terms need to be True; otherwise, the whole formula would evaluate to False.

Compatible Selection 1:

\[ \begin{array}{|c |c |}\hline Variable & Value \\\hline Alpha2.0 & True \\Beta1.3 & True \\Beta1.4 & False \\Gamma0.5 & False \\Gamma0.6 & True \\Gamma0.7 & False \\\hline\end{array} \]

Table 1. Values assigned to each variable as per compatible selection 1

\[ \begin{array}{|c | c |c |}\hline\textbf{Term} & \textbf{Evaluation} & \textbf{Result} \\\hline\text{Alpha2.0} \implies (\text{Beta1.3} \lor \text{Beta1.4}) & \text{True} \implies (\text{True} \lor \text{False}) & \text{True} \\\hline \text{Alpha2.0} \implies (\text{Gamma0.6} \lor \text{Gamma0.7}) & \text{True} \implies (\text{True} \lor \text{False}) & \text{True} \\\hline \text{Beta1.3} \implies (\text{Gamma0.5} \lor \text{Gamma0.6}) & \text{True} \implies (\text{False} \lor \text{True}) & \text{True} \\\hline \text{Beta1.4} \implies \text{Gamma0.7} & \text{False} \implies \text{False} & \text{True} \\\hline \neg (\text{Beta1.3} \land \text{Beta1.4}) & \neg (\text{True} \land \text{False}) & \text{True} \\\hline \neg (\text{Gamma0.5} \land \text{Gamma0.6}) & \neg (\text{False} \land \text{True}) & \text{True} \\\hline \neg (\text{Gamma0.6} \land \text{Gamma0.7}) & \neg (\text{True} \land \text{False}) & \text{True} \\\hline \neg (\text{Gamma0.5} \land \text{Gamma0.7}) & \neg (\text{False} \land \text{False}) & \text{True} \\\hline \text{Alpha2.0} & \text{True} & \text{True} \\\hline\end{array} \]

Table 2. Evaluation of the statement based on compatible selection 1. Since all the terms evaluate to True, the selection is correct.

We can observe in Table 2 that all the terms evaluate to True, which means the selection of the packages is indeed correct and satisfies our requirements.

An Incompatible Selection:

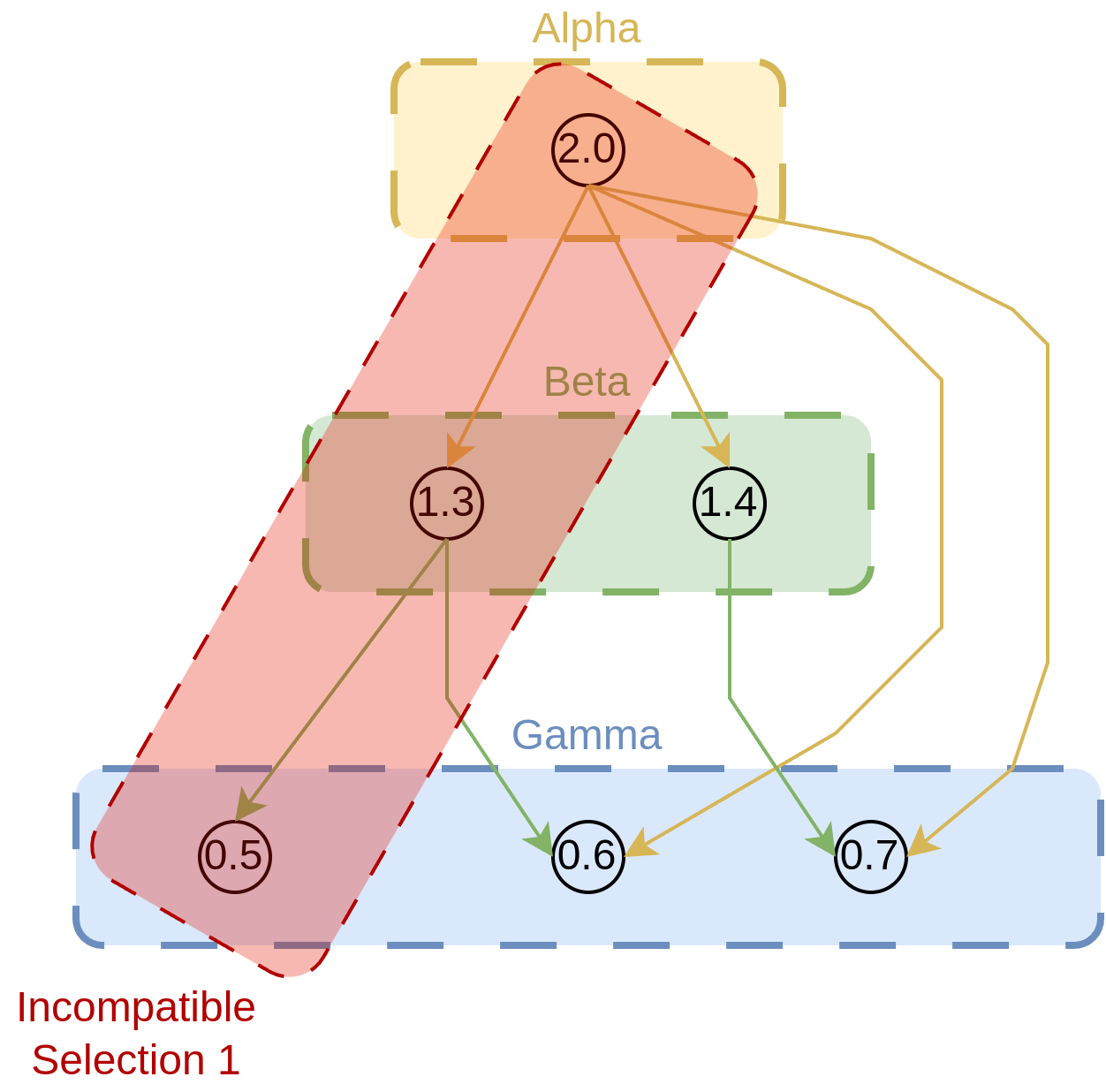
Now, let us try an incompatible selection as visualized in Figure 3, where Gamma-0.5 is selected but Alpha-2.0 depends on Gamma with versions > 0.5, which is contradictory (note that we can select only one version of each package). Let us see how our Boolean formula detects this.

Figure 3. An incompatible selection of packages. It is so because we select Gamma-0.5 but Alpha-2.0 needs Gamma with version > 0.5. As we cannot install multiple versions of the same package, this selection makes it incompatible.

\[ \begin{array}{|c |c |}\hline Variable & Value \\\hline Alpha2.0 & True \\Beta1.3 & True \\Beta1.4 & False \\Gamma0.5 & True \\Gamma0.6 & False \\Gamma0.7 & False \\\hline\end{array} \]

Table 3. Values assigned to each variable as per the incompatible selection in [Figure 3(#__figure-caption_3)].

\[ \begin{array}{|c | c |c |}\hline\textbf{Term} & \textbf{Evaluation} & \textbf{Result} \\\hline\text{Alpha2.0} \implies (\text{Beta1.3} \lor \text{Beta1.4}) & \text{True} \implies (\text{True} \lor \text{False}) & \text{True} \\\hline \text{Alpha2.0} \implies (\text{Gamma0.6} \lor \text{Gamma0.7}) & \text{True} \implies (\text{False} \lor \text{False}) & \text{False} \\\hline \text{Beta1.3} \implies (\text{Gamma0.5} \lor \text{Gamma0.6}) & \text{True} \implies (\text{True} \lor \text{False}) & \text{True} \\\hline \text{Beta1.4} \implies \text{Gamma0.7} & \text{False} \implies \text{False} & \text{True} \\\hline \neg (\text{Beta1.3} \land \text{Beta1.4}) & \neg (\text{True} \land \text{False}) & \text{True} \\\hline \neg (\text{Gamma0.5} \land \text{Gamma0.6}) & \neg (\text{True} \land \text{False}) & \text{True} \\\hline \neg (\text{Gamma0.6} \land \text{Gamma0.7}) & \neg (\text{False} \land \text{False}) & \text{True} \\\hline \neg (\text{Gamma0.5} \land \text{Gamma0.7}) & \neg (\text{True} \land \text{False}) & \text{True} \\\hline \text{Alpha2.0} & \text{True} & \text{True} \\\hline\end{array} \]

Table 4. Evaluation of the statement based on the incompatible selection. Since one term evaluates to False, the whole conjunction will lead to False, and the selection would be marked as incorrect.

We can observe in Table 4 that the formula detects the incompatibility described in Figure 3 as the implication \(Alpha2.0 \implies (Gamma0.6 \lor Gamma0.7)\) becomes False. Selecting Gamma-0.5 makes \(Gamma0.5=True\) and other packages False . As has to be True, the whole term evaluates to False. The task of the package manager is to avoid such assignments.

Now, let us see an unsatisfiable situation that leads to an unsatisfiable instance of the SAT problem.

An unsatisfiable situation

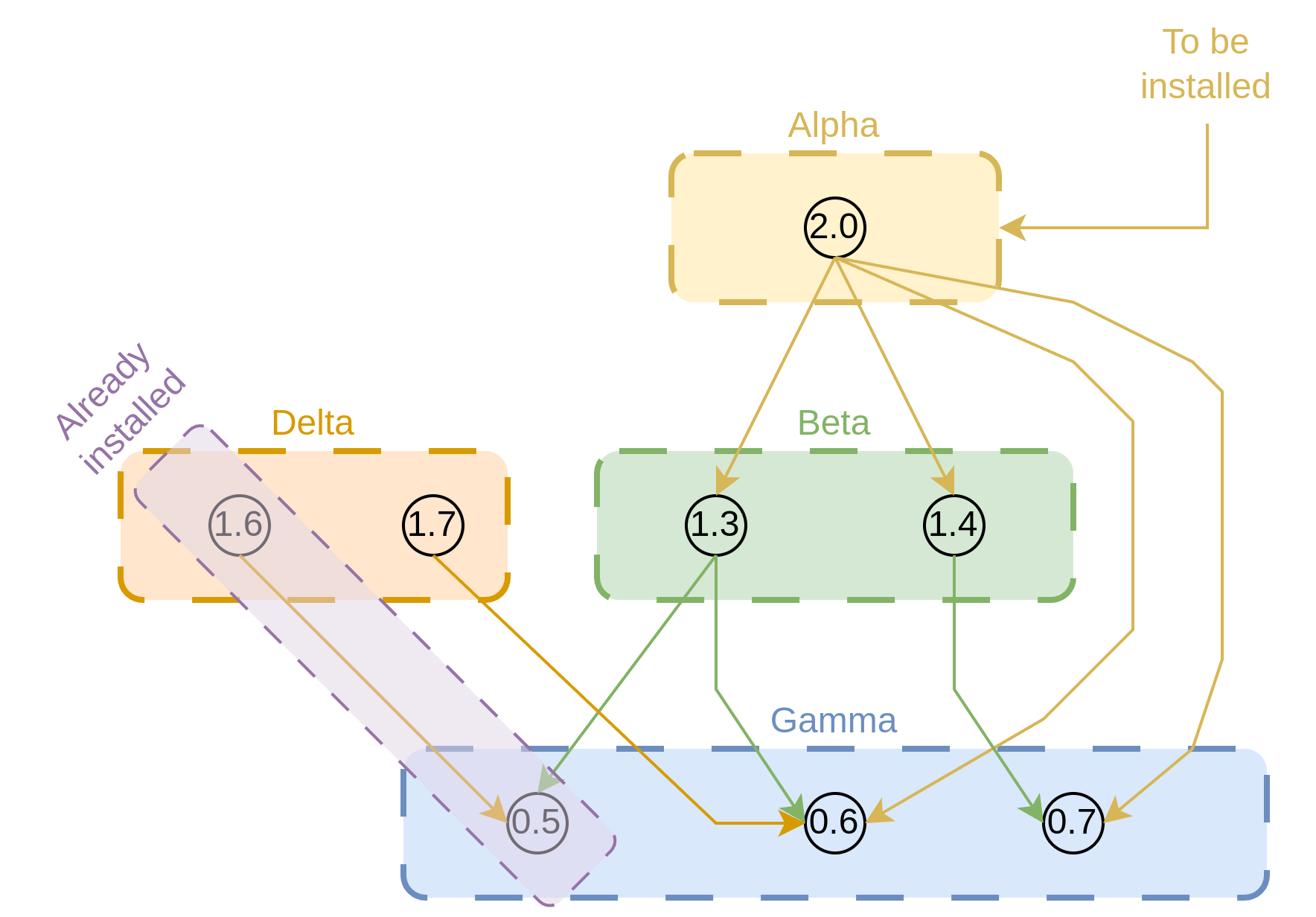
Figure 4. An unsatisfiable situation where Gamma-0.5 is already installed in the system as it is a dependency of the already installed package Delta-1.6. This leads to the incompatible selection as described in Figure 3 as the variable for Gamma-0.6 will always be set to True.

As visualized in Figure 4, let us assume that some package named Delta-1.6, which depends on Gamma-0.5, is already installed in our system, and we now need to install Alpha-2.0. Since Delta-1.6 depends on Gamma-0.5 , \(Gamma0.5\) will always be True. This will lead to the same situation as shown in Figure 3, making this instance of the problem unsatisfiable. In such cases, the package manager would ask the user to upgrade Delta-1.6 to Delta-1.7. If users upgrade Delta, then Gamma-0.5 would be upgraded to Gamma-0.6. This will make the problem satisfiable with the solution same as the 1st compatible selection shown in Figure 2.

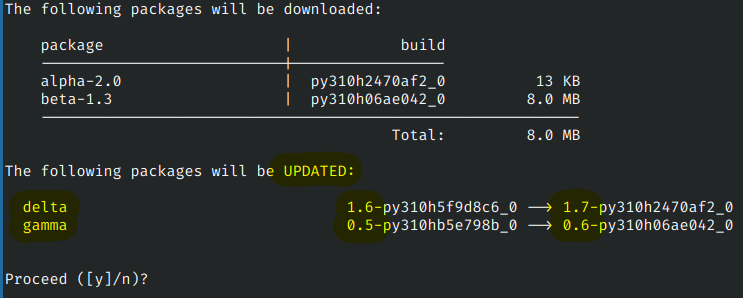
When the conda package manager finds such feasible options, it would prompt the user for such an upgrade, as shown in Figure 5.

Figure 5. A representative example where conda package manager prompts user if it is fine to upgrade delta and gamma in order to install alpha-2.0.

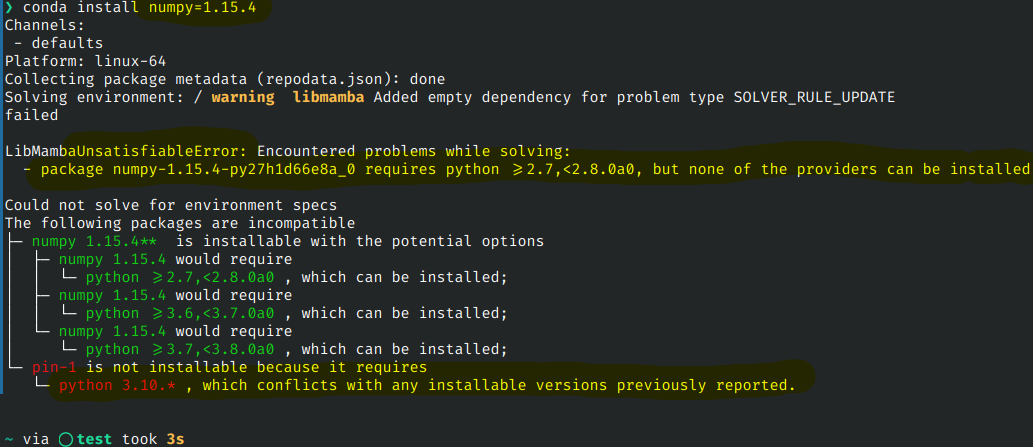
When there is no option for upgrading/downgrading in an unsatisfiable situation, package manager would raise error stating that the requirements are not satisfiable. Check Figure 6 for an example of such a situation with the conda package manager.

Figure 6.Conda raising an unsatifiable error as it finds an unsatisfiable conditions. Th user tries to install numpy-1.15.4 which depends on python with versions >=2.7,<2.8.0a0, >=3.6,<3.7.0a0, and python >=3.7,<3.8.0a0. However, another dependency of numpy is pin-1 depends on python-3.10 which conflicts with the previously reported requirements of python.

Other Satisfiability Problems

There are many other many satisfiability problems that are of interest to computer scientists. We list a couple of them below.

Access Control Policies

Used to define and enforce access rules in computer systems based on roles, permissions, and environmental conditions.

Examples:

• Grant access if the user is an admin or has read permission:
  $ \text{Access} \implies (\text{Admin} \lor \text{ReadPermission})$

• Deny access during lockdown:
  $ \text{Lockdown} \implies \neg \text{ Access }$

• A guest and admin role cannot be assigned together:
  $ \neg (\text{ Guest } \land \text{ Admin })$

Formal Verification

Used to prove correctness of hardware or software components by encoding their behavior and properties as propositional logic formulas.

Examples:

• Verify that a half-adder circuit never outputs Sum = 1 and Carry = 1 when both inputs are zero:
  $ \text{A} = 0 \land \text{B} = 0 \implies \neg (\text{Sum} \land \text{Carry})$

• Negate the property and check if $ \text{A} = 0 \land \text{B} = 0 \land \text{Sum} = 1 \land \text{Carry} = 1$ is satisfiable using a SAT solver.

• If unsatisfiable, the property holds and the circuit behaves correctly in that case.

Course Prerequisites and Scheduling

Used in academic planning tools to ensure students meet course prerequisites and avoid scheduling conflicts.

Examples:

• Taking CS201 requires completing CS101:
  $ \text{CS201} \implies \text{CS101}$

• Prevent scheduling overlap between Bio101 and Chem101:
  $ \neg (\text{Bio101} \land \text{Chem101})$

• Choose only one from three electives:
  $ (\text{E1} \lor \text{E2} \lor \text{E3}) \land \neg (\text{E1} \land \text{E2}) \land \neg (\text{E1} \land \text{E3}) \land \neg (\text{E2} \land \text{E3})$

Resource Management by Operating Systems

Used to manage allocation of resources like CPU, memory, and I/O without conflicts or deadlocks.

Examples:

• A process can run only if it has both CPU and memory available:
  $ \text{Run} \implies (\text{HasCPU} \land \text{HasMemory})$

• Two processes cannot write to the same file simultaneously:
  $ \neg (\text{Write(P1, FileX)} \land \text{Write(P2, FileX)})$

• Deadlock detection rules:
  $ \text{Request(A)} \land \text{Hold(B)} \land \text{WaitsFor(B, A)} \implies \text{PotentialDeadlock}$

Game time !!!

Wan't to try your hand at solving the SAT problem for dependency resolution? Check the following game for more hands-on examples. Check how boolean logic can help in finding constraints.

Game: Package Dependency Resolution Game

Regarding solving the SAT problem

Before discussing solving the SAT problem, first let us discuss verifying if a given solution satisfies the Boolean formula. In the previous section, we verified multiple assignments of boolean variables to check if they satisfy the boolean formula. It can be observed that the number of computations needed to verify the assignment is proportional to the number of operators in it, which is similar to the number of literals in the formula. (NOTE: A literal is some boolean variable \(x_i\) or its negation \(\neg x_i\)).

If we express the time taken to verify the boolean formula with \(n\) literals as the number of computation performed, then the time to verify a SAT formula would be some linear function of \(n\), which would be a polynomial (as we need to iterate though the operands and replace it with result of the operands until we get the final result). We can think of a sequence of operations that can be performed in polynomial time as a fast algorithm (let us refer to the sequence of operations as an algorithm). Such problems are considered to be a part of a class of problems named p. So, verification of a Boolean formula given an assignment comes under the p class of problems.

Now, let us discuss how to find an assignment of the variables. The most naive way would be to try all possible assignments. But this would be exponential in terms of the number of variables. The larger the number of variables, the longer it takes to find an assignment. But, do we have an algorithm that can find an assignment in polynomial time instead of exponential time? Interestingly, the current experience of mathematicians is that there is no such algorithm. However, there exist implementations of heuristic SAT solvers that can find satisfying assignments in a reasonable time, and tons of research is done in developing such algorithms. Discussion of those algorithms is out of the scope of this blog due to my limited knowledge in that area. But, the good news is we can use those implementations to solve our problem of selecting the appropriate dependencies. In addition to this, the implementations also provide recommendations to make the problem satisfiable if it is not, as seen in the situation described in Figure 4. For example, conda uses and implementation called PicoSAT. If you are comfortable in Python, you may check PySAT, which provides an implementation of SAT solvers in Python.

Extras

What is reduction?

If we can transform one problem A into another problem B in polynomial time, we say that problem A is reduced to problem B. If we find a polynomial time algorithm for B, we will have a polynomial time algorithm for A too by first transforming A to B and then solving for B. For example, our problem of finding the correct selection of packages has been transformed into a SAT problem in polynomial time. We just had to write boolean formulas for each condition, and doing so is equivalent to doing tasks with a number of operations as some constant times the number of conditions, which would be linear in the number of conditions.

As of now, we don’t have a polynomial time algorithm for solving the SAT problem, but we saw that given a solution, the verification can be done in polynomial time, and such problems with polynomial time verification are said to be in the class named np. An interesting fact about the SAT problem is that any other problem in np can be reduced to SAT in polynomial time. One such example is our problem of selecting appropriate packages that satisfy all dependencies. That means if we have a polynomial time algorithm to solve SAT, then we have a polynomial time algorithm for all other problems in np. Mathematicians believe that there is no such algorithm, and nobody has been able to prove this yet. But if one can find such an algorithm, then not only will installing a package become fast, but it will also lead to crazy consequences. Check this video for more information on this.